I think I just totally made up this word, “finity”. Google has never heard of it, at least. But it is a word that I thought should be in the English language to describe the properties of a number that is NOT infinite. I’m not so sure the word “affinity” appropriately describes what I’m talking about… regardless… lecture my on vocabulary later. In this blog, I will attempt to put into perspective the extent to which 64-bit memory addressing in computers is NOT infinite, but finite.
When TCP/IP was introduced to the world with a 32-bit address for every computer connected to the internet, not a single soul ever predicted that 4.2 billion IP addresses would not be enough to cover the connected devices all around the world. In the mid 90’s however, the IP-addresses were basically already used up, and static IP addresses were given out sparingly while internet users with multiple devices used NAT gateways to bridge intranets to the internet.
At the same time, when computers started moving to 32-bit memory addressing, no one predicted that computers would ever have more than 4GB of RAM installed. After-all, hard disks were considerably less than 4GB back then. In fact the first IBM PS/2 to come equipped with a 32-bit Intel processor sported just 1 or 2MB of RAM and offered 44MB, 70MB, or 115MB hard-disk options. As I’m sure you’re aware, Hard-disk storage space (the amount of capacity you have to permanently store your photos and videos) is typically considerably larger than RAM installed in your computer (which defines how much data your computer can hold onto at the same time, in a temporary capacity). The top-of-the-line IBM sported a 57:1 Disk/RAM ratio, and I’m sure the 2MB RAM/115MB Hard disk configuration would cost you a pretty penny back then.
| Year | Architecture | Typical RAM | Theroetical Limit:RAM Ratio | Growth | Typical Hard Disk | Theroetical Limit:Disk Ratio | Growth |
|---|---|---|---|---|---|---|---|
| 1987 | 32-bit | 1MB | 4,294 : 1 | 75MB | 55 : 1 | ||
| 2015 | 64-bit | 8GB | 1,152,921,504 : 1 | 8,000 x | 1TB | 9,223,372 : 1 | 13,333 x |
Since then, the standard quantity of RAM loaded onto your average computer has grown 8000 times in size and the Disk size has grown over 13,000 x for a typical system these days. 8-12GB of RAM (8000-12,000MB) being pretty standard for most consumer laptops these days and 1TB Hard-disks (1,000,000MB) being pretty common for hard disks. Servers are a whole other bag which I will not get into.
We started feeling the pinch of the 4GB memory barrier a while ago (the maximum technically addressable by a 32-bit machine), and makers of operating systems, like Windows, and Linux, and Mac OSX eventually had to recompile and retest all their software to work with with larger address models. These days if you buy a laptop or tablet device with more than 2-4GB of ram in it, it invariably has a 64-bit OS loaded on it. But, when, if ever, will we hit the 64-bit barrier?
A 64-bit number can index an awful lot certainly. The highest number that can be computed in 64-bits is 0xFFFFFFFFFFFFFFFF in hexadecimal or 18,446,744,073,909,551,614 in human (decimal) terms. Whereas having this much addressable RAM in your computer would definitely make for a personal computing experience vastly different than what we know of today, this is a VERY finite number. This is not more atoms than there are on planet earth. It is more than there are known stars in the universe, but probably doesn’t account for the unknown ones. It is, however, a number big enough to count every second of time for the next 585 billion years, every millisecond of time for the next 585 million years, or ever microsecond of time for the next 585 thousand years.
It is roughly 4.2 billion Millimeters from San Francisco to Washington DC.
While these numbers are not infinite, it is hard for us humans to wrap out thoughts about such massive quantities of data. Twilight Zone excluded, time is 1-dimensional… and thinking of 1-dimensional data isn’t a very useful, because it is hard for us fathom such large quantities of linear data.
Instead, let’s think about a multi-dimensional problem that we, as humans, can easily relate to.
64-bits is roughly enough to account for 4.2billion squared. By thinking about the limits of 64-bit in the square sense puts it into a perspective that we can understand. For example, it is around 4.2 billion millimeters from San Francisco to Washington DC.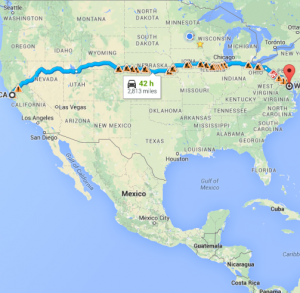 
If we took that and squared it, we would have a chunk of the globe that looked roughly like this:
[IMAGE MISSING]
With 64-bits we can load every square millimeter of this chunk of the earth, assuming our color depth was limited to 8-bits, or one-byte.
8-bits of color data isn’t exactly photo-quality, but it is usable. A 1mm /sq resolution resolution isn’t good enough to read the date off of a penny… although it is a lot of data. If we wanted 32-bit color, we would be able to only handle 1/4th of this picture, so.. only USA west of the center of the Dakotas, excluding Mexico. Still… this is a LOT of data, and it is exciting to think about.
Another way to think of it is like this: There are an estimated 2-billion computers in-use in the world as of this writing. Assuming that all of these 2-billion computers average 8GB of RAM each, we could, with a 64-bit address, assign an individual address for every single byte of ram on every computer in use on planet earth today. Again. This is A LOT of data, but finite. After all, this is not enough address space to account for all the Hard-disk storage on planet earth, for which there is roughly 2-trillion gigabytes, by my guesstimation. This is more than 10,000 times the amount of data that is addressable by a 64-bit number.
2,000,000,000,000,000,000,000,000
> 18,446,744,073,909,551,614
One thing is for certain. As the world moves closer and closer to these limits, humans are going to rely more and more on computer algorithms, and dare-I-say, artificial intelligence, simply to deal with the intricacies of possessing all this data. And computer programmers are going to have to work on an increasingly macroscopic level in the future in order to search, validate, and catalog all this data.
Finally, to further put this into perspective… what if we were dealing with volumetric data? My calculator won’t tell me what the cube-root of a 64-bit number is, but it will tell me what it is for 63-bits. 63-bits can address roughly 2.097 km of data cubed at a 1mm ^3 resolution. This, dare I say, is very finite. If you want nanometer resolution (for microscopes) then you’re limited to a mere 2mm cubed region of data.
What will the world of computers look like when we’re pushing the boundaries of these limits? I dunno. I know that it is fun to ponder, however.
That was really thought-provoking! It’s fascinating to imagine what the future of computing might look like as we approach these limits. I wonder, with the advent of quantum computing, will we start seeing machines capable of processing even larger quantities of data? Also, how do you think operating systems and programming languages will have to adapt to accommodate these changes? I’m curious to hear your thoughts on this.
Quantum computing is a game-changer, absolutely! The shift from bits to qubits already strains our mental models about data. Operating systems and programming languages are definitely going to evolve. Maybe we’ll see more languages that inherently support parallel processing and quantum algorithms? What’s exciting is imagining how we’ll handle such shifts on a conceptual level, straight down to the coding practices. Have you seen any emerging tech that suggests how OSes might adapt?
You’re spot on about the exciting shift. There are hints at more quantum-resistant cryptographic algorithms being integrated into operating systems today. Also, some programming languages are incorporating concepts like entanglement which is a step towards accommodating quantum computing principles. It’s going to be fascinating to see how these adaptations unfold and what new paradigms emerge!